AI摘要:通过降维并利用几何结构,分析高维嵌入空间的螺旋形态,结合多路径遍历和排序策略,成功还原隐藏的 Flag:“HTB{L0ST_1N_TH3_SP1R4L}”。
目标
- 输入:
embeddings.npy(高维嵌入,形如 110×512)、tokens.npy(对应字符数组)。 - 方法:PCA 将嵌入降维到 2D/3D,依据点的几何结构(环形/螺旋),按合适顺序遍历并拼接字符。
步骤 1:理解数据与挑战
embeddings.npy:每个字符在高维空间的向量表示;tokens.npy:字符集合(含字母、数字、符号),在空间中“打散”分布;- 思路:降维后,数据通常呈现环形/螺旋等结构。沿着该结构遍历点,即可恢复字符原始顺序,拼接得到可读字符串与 Flag。
步骤 2:确定如何完成
机器无法像人类一样理解词语的含义,因此我们需要将词语转换为它们可以“操作”的形式——也就是数字。
在自然语言处理中,代币(token)是句子的最小单元,它可以是单词、子词,甚至是单个字符。例如,句子“天空是蓝色的”可以被拆分为“天空”、“天”、“是”和“蓝色”等代币。
每个代币都会被映射为一个向量 ID,该向量的每一维都包含数值信息,用来捕捉代币的特征与关系。例如,“蓝色”这个词可能对应向量 [0.23, 0.89, 0.99, 0.98, ...]:
- 第一维可以表示与“火”的相似度(因此数值较低);
- 第三维可能表示与“颜色”的相关性(因此数值接近1)。
这些向量就是嵌入(embedding)——一种数值化表示,使机器能够理解语言的语义信息。
但是,这类向量通常维度很高,可能达到100或1000维,我们无法直观地进行可视化。因此,我们需要将高维向量降维到可视化友好的三维空间。幸运的是,scikit-learn 提供了 PCA(主成分分析) 方法,可以有效地将高维数据压缩到低维,同时尽量保留数据的主要特征。
本次挑战提示中提到“3D”和“阴影”,这正暗示我们可以将向量降到三维空间进行可视化,以便更直观地观察代币之间的关系。
首先让我们来将矢量尺寸缩小至三维,并绘制出矢量及其2D阴影。
image.py
#!/usr/bin/env python3
# 保存为 find_flag_in_png.py
import sys, os, re
from PIL import Image
import numpy as np
def find_ascii_in_bytes(b, minlen=6):
cur = bytearray()
res = []
for x in b:
if 32 <= x < 127:
cur.append(x)
else:
if len(cur) >= minlen:
res.append(cur.decode('latin1'))
cur = bytearray()
if len(cur) >= minlen:
res.append(cur.decode('latin1'))
return res
def search_patterns_in_strings(strings):
hits = []
for s in strings:
for m in re.finditer(r'(flag\{.*?\}|FLAG\{.*?\}|ctf\{.*?\}|CTF\{.*?\})', s, flags=re.IGNORECASE):
hits.append(m.group(0))
return hits
def lsb_extract_and_search(img_arr, max_bytes=200000):
H,W = img_arr.shape[0], img_arr.shape[1]
C = img_arr.shape[2] if img_arr.ndim==3 else 1
# 每像素交织的最低有效位(LSB)(R,G,B,R,G,B,...)
bits = []
if C == 1:
data = img_arr.ravel()
bits = (data & 1).astype(np.uint8)
else:
# 形状 H,W,C -> 逐像素迭代
# 为限制内存/时间,仅采样前 N 个像素
Npix = min(H*W, 20000) # sample first 20k pixels
pix = img_arr.reshape(-1, C)[:Npix]
bits = (pix & 1).reshape(-1)
# 组装字节(高位在前,MSB-first)
nbytes = (len(bits) // 8)
bytes_arr = []
for i in range(nbytes):
byte = 0
for j in range(8):
bit = int(bits[i*8 + j])
byte = (byte << 1) | bit
bytes_arr.append(byte)
b = bytes(bytes_arr)
text = ""
try:
text = b.decode('utf-8', errors='ignore')
except:
text = b.decode('latin1', errors='ignore')
hits = search_patterns_in_strings([text])
return hits, text[:1000]
def per_channel_lsb_search(img_arr):
hits = []
snippets = {}
if img_arr.ndim==3:
C = img_arr.shape[2]
for ch in range(C):
data = img_arr[:,:,ch].ravel()
bits = (data & 1).astype(np.uint8)
nbytes = len(bits)//8
if nbytes == 0: continue
bytes_arr = []
for i in range(nbytes):
byte = 0
for j in range(8):
bit = int(bits[i*8 + j])
byte = (byte << 1) | bit
bytes_arr.append(byte)
b = bytes(bytes_arr)
s = b.decode('latin1', errors='ignore')
found = re.findall(r'(flag\{.*?\}|FLAG\{.*?\}|ctf\{.*?\}|CTF\{.*?\})', s, flags=re.IGNORECASE)
if found:
hits.extend(found)
snippets[f'channel_{ch}'] = s[:500]
return hits, snippets
def main(path):
if not os.path.exists(path):
print("file not found:", path); return
with open(path, 'rb') as f:
raw = f.read()
print("[*] raw bytes length:", len(raw))
# 1)原始 ASCII 字符串
strings = find_ascii_in_bytes(raw, minlen=6)
print("[*] ascii-string snippets found in file bytes (first 40):")
for s in strings[:40]:
print(" ", s[:200])
# 在原始 ASCII 中搜索可能的 flag 模式
raw_hits = search_patterns_in_strings(strings)
if raw_hits:
print("[+] FOUND flag-like patterns in raw bytes:", raw_hits)
else:
print("[-] No explicit flag{...} pattern found in raw file bytes.")
# 2)通过 PIL 检查 PNG 文本块
try:
im = Image.open(path)
print("[*] Image format/mode/size:", im.format, im.mode, im.size)
print("[*] Image info keys:", im.info.keys())
for k,v in im.info.items():
print(" info:", k, "=", str(v)[:400])
arr = np.array(im)
except Exception as e:
print("PIL open error:", e)
return
# 3)每像素交织的 LSB
print("[*] Running LSB per-pixel interleaved search (sampled). This can take a moment...")
hits, snippet = lsb_extract_and_search(arr)
if hits:
print("[+] LSB per-pixel hits:", hits)
else:
print("[-] no flag-like patterns in interleaved LSB. snippet preview:")
print(snippet[:400])
# 4)逐通道 LSB
ch_hits, ch_snips = per_channel_lsb_search(arr)
if ch_hits:
print("[+] LSB per-channel hits:", ch_hits)
else:
print("[-] no flag found by per-channel LSB. channel snippets shown below.")
for k,v in ch_snips.items():
print(" ", k, "->", v[:200].replace('\n',' '))
print("[*] Done.")
if __name__ == "__main__":
if len(sys.argv) < 2:
print("Usage: python3 find_flag_in_png.py file.png")
else:
main(sys.argv[1])得到矢量图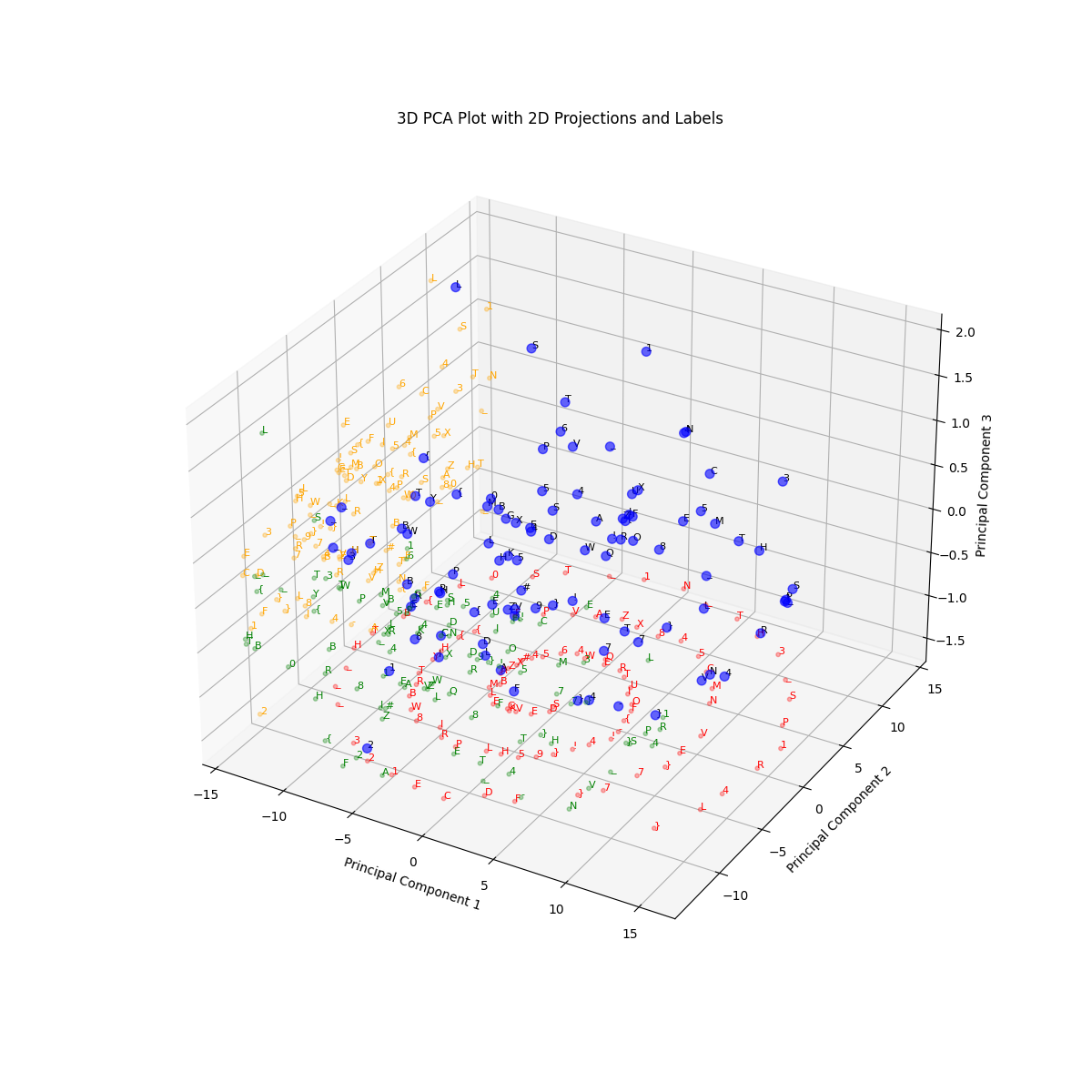
你注意到这其中有什么不寻常的地方吗?
在 XY 平面上的那些螺旋纹理太过整齐,绝非巧合。
步骤 3:确定方案
- 加载数据并将 tokens 统一为可拼接的字符串。
- 用 NumPy 的 SVD 实现 PCA,将高维嵌入投影到 3 维。
- 生成候选字符串:
- 主轴排序:分别按 PC1/PC2/PC3 升序与降序拼接。
- 极角排序:在 PC1–PC2 、 PC1–PC3 、 PC2–PC3 平面按 atan2 角度遍历。
- 2D 最近邻路径与 MST+DFS 遍历,得到路径式拼接。
pwn.py
import numpy as np
def load_data():
E = np.load('embeddings.npy')
T = np.load('tokens.npy', allow_pickle=True)
# 将不同类型的 token 规范化为普通 Python 字符串
norm_tokens = []
for t in T:
if isinstance(t, bytes):
norm_tokens.append(t.decode('utf-8', errors='ignore'))
else:
norm_tokens.append(str(t))
return E, np.array(norm_tokens)
def pca_numpy(E, k=2):
# 进行均值中心化并用 SVD 投影(无需 sklearn 的 PCA)
E0 = E - E.mean(axis=0, keepdims=True)
U, S, Vt = np.linalg.svd(E0, full_matrices=False)
return E0 @ Vt[:k].T
def join_tokens(T, order):
return ''.join(T[order])
def angle_sort(X2):
angles = np.arctan2(X2[:, 1], X2[:, 0])
return np.argsort(angles)
def nearest_neighbor_order(X2):
n = X2.shape[0]
visited = np.zeros(n, dtype=bool)
start = np.argmin(X2[:, 0]) # 最左侧点作为起点
order = [start]
visited[start] = True
for _ in range(n - 1):
last = order[-1]
# 计算到所有未访问点的距离
idxs = np.where(~visited)[0]
diffs = X2[idxs] - X2[last]
dists = np.einsum('ij,ij->i', diffs, diffs)
next_idx = idxs[np.argmin(dists)]
visited[next_idx] = True
order.append(next_idx)
return np.array(order)
def mst_dfs_order(X2, start=None):
n = X2.shape[0]
if start is None:
start = np.argmin(X2[:, 0])
# 计算完整的距离矩阵
diffs = X2[:, None, :] - X2[None, :, :]
dists = np.einsum('ijk,ijk->ij', diffs, diffs)
visited = np.zeros(n, dtype=bool)
visited[start] = True
edges = [[] for _ in range(n)]
for _ in range(n - 1):
# 在已访问集合与未访问集合之间寻找最短边
best_i = -1
best_j = -1
best_d = np.inf
for i in np.where(visited)[0]:
# 仅考虑通向未访问节点的边
j_candidates = np.where(~visited)[0]
if j_candidates.size == 0:
continue
j = j_candidates[np.argmin(dists[i, j_candidates])]
d = dists[i, j]
if d < best_d:
best_d = d
best_i = i
best_j = j
# 将该边加入最小生成树(MST)
edges[best_i].append(best_j)
edges[best_j].append(best_i)
visited[best_j] = True
# 从起点进行 DFS 遍历
order = []
stack = [start]
seen = np.zeros(n, dtype=bool)
while stack:
node = stack.pop()
if seen[node]:
continue
seen[node] = True
order.append(node)
# 邻居按距离由近到远入栈,使路径更平滑
nbrs = edges[node]
if nbrs:
nbrs_sorted = sorted(nbrs, key=lambda j: dists[node, j], reverse=True)
stack.extend(nbrs_sorted)
return np.array(order)
def nearest_neighbor_order_start(X, start):
n = X.shape[0]
visited = np.zeros(n, dtype=bool)
order = [int(start)]
visited[start] = True
for _ in range(n - 1):
last = order[-1]
idxs = np.where(~visited)[0]
diffs = X[idxs] - X[last]
dists = np.einsum('ij,ij->i', diffs, diffs)
next_idx = idxs[np.argmin(dists)]
visited[next_idx] = True
order.append(int(next_idx))
return np.array(order)
def path_length(order, X):
diffs = X[order[1:]] - X[order[:-1]]
dists = np.sqrt(np.einsum('ij,ij->i', diffs, diffs))
return float(dists.sum())
def two_opt_improve(order, X, max_iter=2000):
n = len(order)
improved = True
it = 0
best = order.copy()
best_len = path_length(best, X)
while improved and it < max_iter:
improved = False
it += 1
for i in range(1, n - 2):
for k in range(i + 1, n - 1):
# 当前考虑的两条边:(i-1,i) 与 (k,k+1)
a, b = best[i - 1], best[i]
c, d = best[k], best[k + 1]
old = np.linalg.norm(X[a] - X[b]) + np.linalg.norm(X[c] - X[d])
new = np.linalg.norm(X[a] - X[c]) + np.linalg.norm(X[b] - X[d])
if new + 1e-9 < old:
best[i:k + 1] = best[i:k + 1][::-1]
best_len -= (old - new)
improved = True
# 若本轮没有改进则提前退出循环
return best
def get_flag_substring(s):
start = s.find('HTB{')
if start == -1:
return None
end = s.find('}', start + 4)
if end == -1:
return None
return s[start:end + 1]
def main():
E, T = load_data()
print('Embeddings shape:', E.shape, 'Tokens count:', len(T))
# 使用 SVD‑PCA 将数据投影到 3 维
X3 = pca_numpy(E, k=3)
# 分别沿每个主成分轴进行升序/降序排序
candidates = []
for i in range(3):
order = np.argsort(X3[:, i])
asc = join_tokens(T, order)
desc = join_tokens(T, order[::-1])
print(f'PC{i+1} asc:', asc)
print(f'PC{i+1} desc:', desc)
candidates.append(asc)
candidates.append(desc)
# 在多组主成分平面上进行基于极角的 2D 排序(环绕遍历)
def angle_sort_pair(X3, i, j):
X2 = np.stack([X3[:, i], X3[:, j]], axis=1)
order = angle_sort(X2)
return join_tokens(T, order), join_tokens(T, order[::-1])
for (i, j) in [(0, 1), (0, 2), (1, 2)]:
asc, desc = angle_sort_pair(X3, i, j)
print(f'Angle axes ({i+1},{j+1}) asc:', asc)
print(f'Angle axes ({i+1},{j+1}) desc:', desc)
candidates.append(asc)
candidates.append(desc)
# 在 2D 投影上使用贪心的最近邻路径
# 使用前两个主成分上的最近邻来获得路径式排序
X2 = X3[:, :2]
order_nn = nearest_neighbor_order(X2)
nn = join_tokens(T, order_nn)
nn_rev = join_tokens(T, order_nn[::-1])
print('Nearest path:', nn)
print('Nearest path reverse:', nn_rev)
candidates.append(nn)
candidates.append(nn_rev)
# 使用 2‑opt 对最近邻路径进行优化
order_nn_opt = two_opt_improve(order_nn, X2)
nn_opt = join_tokens(T, order_nn_opt)
nn_opt_rev = join_tokens(T, order_nn_opt[::-1])
print('Nearest path (2-opt):', nn_opt)
print('Nearest path (2-opt reverse):', nn_opt_rev)
candidates.append(nn_opt)
candidates.append(nn_opt_rev)
# 基于最小生成树的 DFS 路径
order_mst = mst_dfs_order(X2)
mst = join_tokens(T, order_mst)
mst_rev = join_tokens(T, order_mst[::-1])
print('MST DFS path:', mst)
print('MST DFS path reverse:', mst_rev)
candidates.append(mst)
candidates.append(mst_rev)
# 以字符 'H' 的位置为起点搜索路径
H_idxs = [i for i, tok in enumerate(T) if tok == 'H']
best_flag = None
for h in H_idxs:
path_h = nearest_neighbor_order_start(X2, h)
path_h_opt = two_opt_improve(path_h, X2)
s_h = join_tokens(T, path_h_opt)
candidates.append(s_h)
f = get_flag_substring(s_h)
if f and (best_flag is None or len(f) > len(best_flag)):
best_flag = f
if best_flag:
print('Best flag by H-start two-opt:', best_flag)
# 尝试提取 HTB 格式的 Flag 子串
print('\nCandidate flags found:')
printed = set()
for s in candidates:
f = get_flag_substring(s)
if f and f not in printed:
printed.add(f)
print(f)
if __name__ == '__main__':
main()步骤 4:确认最终 Flag
- 结合数据在低维空间呈现的“螺旋”结构与候选的语义:
HTB{L0ST_1N_TH3_SP1R4L}该串读作 “LOST IN THE SPIRAL”,与题意贴合。
关键实现要点(速览)
PCA(SVD):仅做“均值中心化”,若特征量纲差距大,建议在 PCA 前加入“单位方差标准化”(可选):
E_std = (E - mean) / (std + 1e-8)。
排序策略:
- 主轴排序:按各主成分坐标升/降序;
- 极角排序:在多个主成分平面上按
atan2角度排序; - 最近邻路径:在 2D 投影上从初始点依次连接最近未访问点;
- two?opt:两点交换优化路径,减少折返;
- MST+DFS:用最短边连通全图,再做 DFS 获得平滑遍历序列。
- 自动提取:对每个候选字符串查找
HTB{...}子串,去重后打印。
结语
遵循本教程从数据投影、几何遍历到子串提取的流水线,即可稳健地还原被“丢失在超空间”的字符序列,并快速定位 HTB Flag。


评论 (0)